跳至主要內容

递归

xmut-lby大约 17 分钟

递归

递归本不应该放在我们这个课程上讲。但鉴于我们大家面对的严峻现实（指你们很菜）。为了后续的课程，有必要再强调一下。

本章上方阅读时间写的是17分钟，但实际上我写了快一周，比平常的章节要长得多。并且改了很多次，让这个数字从15上升到16再上升到17。 所以我已经尽力了，现在是看你们的时候了！

首先必须为你们说句话：一时转不过弯来理解不了递归并不是你们的问题。彼得·多伊奇(L Peter Deutsch)在《程序员修炼之道》(The Pragmatic Programmer)一书里说：To Iterate is Human, to Recurse, Divine。也就是说迭代是属于凡人的，而递归属于神的。所以任何人一开始无法理解递归都不是多大的错——错在于认为它不可能被理解。

当然这句话也说明一个道理——递归是极其强大的工具，计算机方向的学生必须掌握。

什么是递归

递归是自己调用自己——请你们暂时忘掉这句没用的废话。我们以著名的阶乘为例来看一看迭代和递归这两种不同的思维方式：

迭代式：

n!=1×2×3×...×n n! = 1\times 2\times 3\times ... \times n

因此我们求这个值的计算过程是：

for( int i=1; i<n; ++i ){
    factorial *= i;
}

或者说，计算过程是这样的：

  1. 计算f(1)
  2. 根据f(1)计算f(2)
  3. 根据f(2)计算f(3) ...

直到计算f(n)

这是迭代的思维方式，我有一个明确的从1开始的公式，沿着这个公式逐步增长，直到n为止，非常符合我们对循环的理解。

如果我们将结果看作终点，那么迭代式思维从最初的起点（11）开始，走第一步（22），走第二步（33），一步步走到终点（nn），最符合我们的直觉。

递归式的理解则是反过来的：

n!=(n−1)!×n(n−1)!=(n−2)!×(n−1)(n−2)!=(n−3)!×(n−2)...3!=2!×32!=1!×21!=1 \begin{align*} n!&=(n-1)!\times n \\ (n-1)!&=(n-2)!\times (n-1) \\ (n-2)!&=(n-3)!\times (n-2) \\ ... \\ 3!&=2!\times 3 \\ 2!&=1!\times 2 \\ 1!&=1 \\ \end{align*}

递归的理解是从重点开始的，先看到终点前一步（n−1n-1）如何走到终点（nn），再看到终点前两步（n−2n-2）如何走到终点前一步（n−1n-1），然后以此类推。

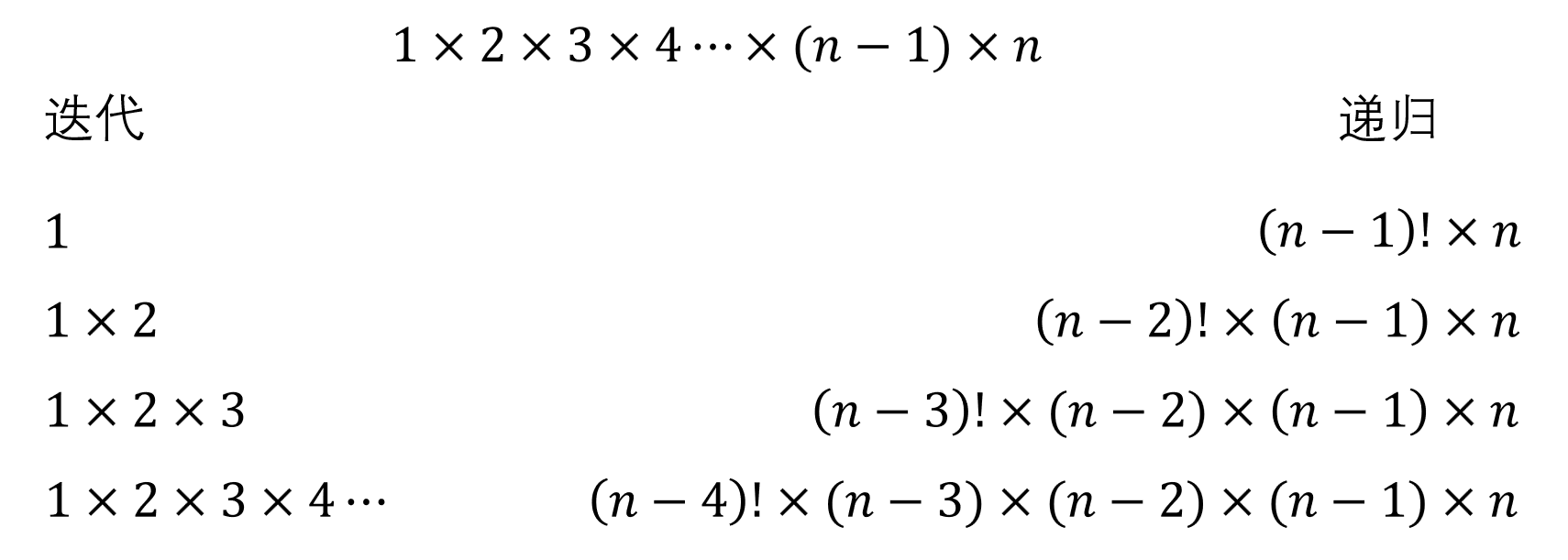
迭代 v.s. 递归
迭代 v.s. 递归

这对于很多人来说就转不过弯来，我还没走到n−1n-1呢，怎么就考虑怎么从n−1n-1走到nn呢？但这点也正是递归精妙和最有用的地方！

到这里我们就要请出大家中学年代的老朋友了：

数学归纳法

回忆一下你如何使用数学归纳法的：

  • (a).证明f(1)f(1)正确。
  • (b).（假设）f(k)f(k)时命题正确  ⟹  \implies f(k+1)f(k+1)也正确。

这样命题就可以证明了。

当初我们学这里的时候，总感觉怪怪的——怎么就只证明这两个就行了呢？中间的证明步骤呢？

然而实际上数学归纳法在逻辑上是无懈可击的：

  1. f(1)f(1) 根据(a)显然成立
  2. 由f(1)f(1)成立和(b)，f(2)f(2)也成立
  3. 由2和(b)，f(3)f(3)成立
  4. 由3和(b)，f(4)f(4)成立 ...

所以对所有的nn，不管nn有多大，命题都成立。

也就是说，实际上中间从22到n−1n-1的所有步骤，都可以由上面的逻辑自动导出。

那么我们再回过头看我们的递归，用递归的方式如何写阶乘：

递归 v.s. 数学归纳法

int factorial( int n ){
    if( n == 1 ){
        return 1;                 // (a)
    }
    return n*factorial(n-1);      // (b)
}

再对照一下上面数学归纳法的定义，是不是非常相似？

  • (a). 当n==1时，函数返回1。
  • (b). 当n!=1时，通过f(n-1)递推。

所以递归在逻辑上也是无懈可击的：

  1. f(1) 根据(a)可以得到
  2. 由f(1)的值和(b)，f(2)可以得到
  3. 由2和(b)，f(3)也可以得到
  4. 由3和(b)，f(4)也可以得到 ...

一直到你想要的f(n)为止，都可以通过这一过程得到。

等下！你肯定要说，我并没有写这些代码啊，怎么就能得到了？！

因为计算机可以根据你的代码自动导出！准确说，上面从1到n的计算过程，必然是都要做的没错。但你只要写好了递归函数，代码执行的过程中一定会把上面的所有计算过程都算过一遍，而这一切都可以自动完成。

那么我们再回去看递归对应的两个条件：

(b)这个条件给定的是如何从f(n-1)如何得到f(n)，也就是所谓的递推式。这是递归可以实现向下推导的基本条件。

而(a)这个条件，你可以视为停机条件——请记住，递归的逻辑是从后往前的推导的。也就是说，从n开始，到1结束。

所以写递归函数实际上是非常简单的事，甚至可以说比迭代解法更简单：

  1. 写出f(1)的情况。
  2. 写出如何从f(n-1)到f(n)的递推形式
  3. 结束

这是递归的第一层理解：写好停机条件和递推式，递归会自动完成。

为什么必须递归

到此为止的部分可能能让你写出正确的递归函数，但无法解答一个问题：为什么我们必须使用递归。

毕竟无论是阶乘还是斐波拉契数列，迭代解法都比递归更容易理解——而且实际上——更快。在生产环境中，递归通常是最后的选择，因为其开销和效率都不尽如人意。

那么为什么我们还要学习并使用它？因为某些场合下它几乎是唯一的选择，我们再回顾下前面看到的迭代的解法：

  1. 计算f(1)
  2. 根据f(1)计算f(2)
  3. 根据f(2)计算f(3) ...

直到计算f(n)

这个步骤里实际上对递推的过程是有隐含要求的：

  1. f(1)必须明确可计算，也就是起始条件必须明确。
  2. 计算f(n)所需的f(n-1)是可预测的，最好是明确只有一条。

如果把这两条规则放到阶乘里，我们会发现它都满足，所以阶乘用迭代解是轻松愉快的。

而如果把这两条规则放到斐波拉契数列里，第一条也是满足的，第二条却并不满足。 但我们可以巧妙地利用缓存状态的方式绕开它——是的，斐波拉契数列的算法不是简单的迭代解法，而是可以归入动态规划（DP）的范畴。

但对于某些情况，这两个条件就不一定满足了。

举一个你们很熟悉的例子，你们一定都听说过这个故事：

递归小故事

从前有座山，山里有座庙，庙里有一个老和尚和一个小和尚。有一天老和尚对小和尚说：

从前有座山，山里有座庙，庙里有一个老和尚和一个小和尚。有一天老和尚对小和尚说：

从前有座山，山里有座庙，庙里有一个老和尚和一个小和尚。有一天老和尚对小和尚说：

...

这实际上就是一个递归。

当我们把对小和尚说这段，放在说的内容的前面时，我们可以如上面那样用迭代的方式写出这段话，一直到结束（如果能结束的话）。

但是，如果我要求把说的内容往前面放时，你还能写出来吗？也就是：“blablabla”，老和尚对小和尚说道这种形式，你还能用迭代的方法写出来吗？

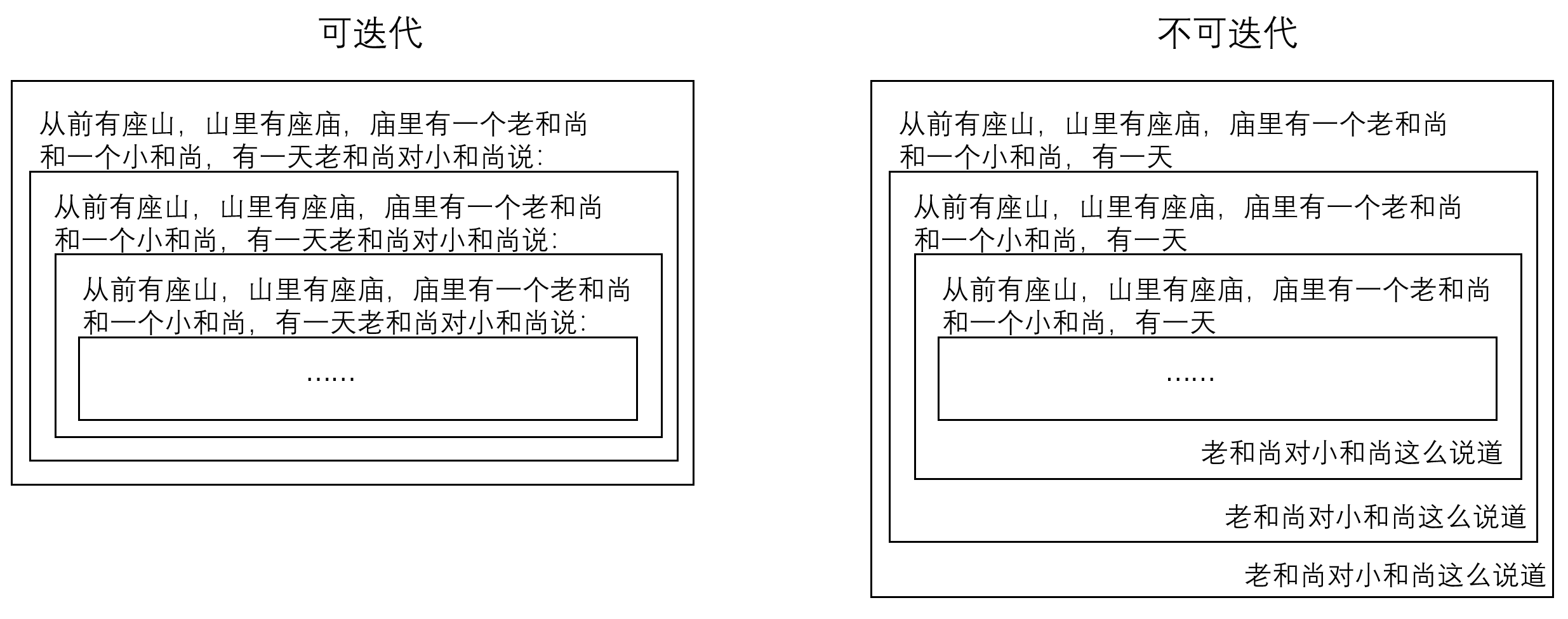
可迭代的递归和不可迭代的递归
可迭代的递归和不可迭代的递归

下面是一些具体一些的例子

反转字符串

你们可能做过反转字符串的题目。解法也非常容易理解：

void reverse_string( const char* s ){
    int len = strlen(s);             // 获得字符串长度
    for( int i=len-1; i>=0; --i ){
        printf("%c", s[i]);          // 从后往前打印，实现反转
    }
    printf("\n");
}

但我们对这个题目的要求稍微难亿点点——只能遍历一趟的情况下，要如何实现反转？这种情况就是无法确认f(1)的情况——你不跑完一趟是无法知道f(1)的。

但如果用递归的思维方式就很好理解：

  1. 停机条件——遇到\0
  2. 反转当前字符串（f(n)）等于反转除当前字符之外的剩余字符串（f(n-1)）+打印当前字符。
void reverse_string( const char* s ){
    if( *s == '\0' ){
        printf("\n");
        return;          // 停机条件
    }
    reverse_string(s+1); // f(n-1)
    printf("%c",*s);     // 打印当前字符
}

在这个例子里，f(1)无法直观地得到，只能随着递归的展开最后才能确定，递归就比迭代容易实现。

汉诺塔

汉诺塔是另一个典型的（对于目前的你们）只能用递归解决的问题。

汉诺塔问题上，不仅仅确定f(1)也就是初始条件很难，确定每个步骤的状态f(n)以及如何从前一个状态达到f(n)这个状态都很难。

也就是说，正向是很难处理的。但如果反过来，从后往前以递归的方式考虑，则容易思考的多：

  1. 停机条件：只剩下一个块，直接从源杆移动到目标杆即可
  2. 递推公式（f(n)）：把上面的n-1个盘子从源杆移动到空闲杆（f(n-1)），把第n个盘子从源杆到目标杆，再移动n-1个盘子从空闲杆移动到目标杆（f(n-1)）。

这里从递推公式里也可以看出为什么正向推导很难：我们需要执行两次f(n-1)才能得到f(n)。如果我们用图来表示的话是这样：

也就是说每往下一层，函数执行次数的增长是以指数增长的。这也是为什么这类问题迭代解法难写的原因之一——越接近停机条件，它的状态越多，你的推导会以指数级增长。

但反过来，以递归的角度看，它的起始状态是确定的，反而是存在一个非常明确的起点。至于推导的过程——让程序自己按停机条件算就完事了。

我们给出汉诺塔的C代码：

void hanoi_tower( int discs, char from, char to, char idel ){
    if( discs == 1 ){         // 停机条件
        printf("%c->%c\n", from, to );
        return;
    }
    hanoi_tower( discs-1, from, idel, to ); // 把n-1个盘从from搬到idel
    printf("%c->%c\n", from, to );         // 把第n个盘从from搬到to
    hanoi_tower( discs-1, idel, to, from ); // 把n-1个盘从idel搬到to
}

请大家对照上面的算法描述，是不是就对照着来写的。

另外有一种更简洁的写法，大家可以思考下为什么这种写法也正确：

void hanoi_tower( int discs, char from, char to, char idel ){
    if( discs == 0 ){         // 停机条件
        return;
    }
    hanoi_tower( discs-1, from, idel, to ); // 把n-1个盘从from搬到idel
    printf("%c->%c\n", from, to );         // 把第n个盘从from搬到to
    hanoi_tower( discs-1, idel, to, from ); // 把n-1个盘从idel搬到to
}

其他问题

C语言OJ里的递归子标签下已经有足够多的问题了，请大家自行尝试（然而只有3个ac提交）。

这里对其中的两个问题做个简单的讲解。

欧几里得法求最大公约数

这个问题可以描述为：

  1. 取m，n中较大的那个数，不妨设较大数为m，令m/n，得到余数r。
  2. 如果余数为0，那么两者最大公约数就是n（较小的那个）。
  3. 如果余数不为0，就对n，r重复上面的过程

这可以看作一个迭代式的描述，我们可以根据这一算式写出代码：

int gcd( int m, int n ){
	if( n>m ){
		swap(m,n);
	}
    while( n != 0 ){
        int r = m%n;
        m = n;
        n = r;
    }
    return m;
}

然而，如果从递归的角度去考虑的话：

  1. 停机条件：m可以被n整除，此时返回n
  2. 递推公式：如果m不能被n整除，则fn(m,n)=fn−1(n,m%n)f_{n}(m,n) = f_{n-1}(n,m\%n)

用递归去写这个代码，你会发现逻辑远比前面的迭代法简洁。

迷宫求解

这个问题也可以转换为以下的递归式解法：

  1. 停机条件：当前格就是出口，或者已经无路可走。
  2. 递推公式：当前格到迷宫出口有路 = 与当前格相邻的周围格到迷宫出口有路

当然本题的难度在于你必须标记你当前已经走过的路径，否则你会反复走从A->B，再从B->A这样死循环。 最简单的处理方式就是给已经走过的路径染色（打标记），保证探索新路径时不会走回老路。

递归的第二层理解

当上面的题目你都掌握之后，你应该不再惧怕递归了。并且会开始跃跃欲试用递归解决问题。因为你会发现“写好停机条件和递推式，递归会自动完成”这个性质简直太棒了。

然而我们还是要问：

代价是什么
代价是什么

这个问题只有真正理解了递归在计算机中是如何执行的，你才能真正回答。

递归如何执行

我们以汉诺塔为例来说明整个调用过程，假如我们要将3个盘子从A移动到B。

那么调用就是：h( 3, A, B, C );

整个运行过程可以用下面的图来表示：

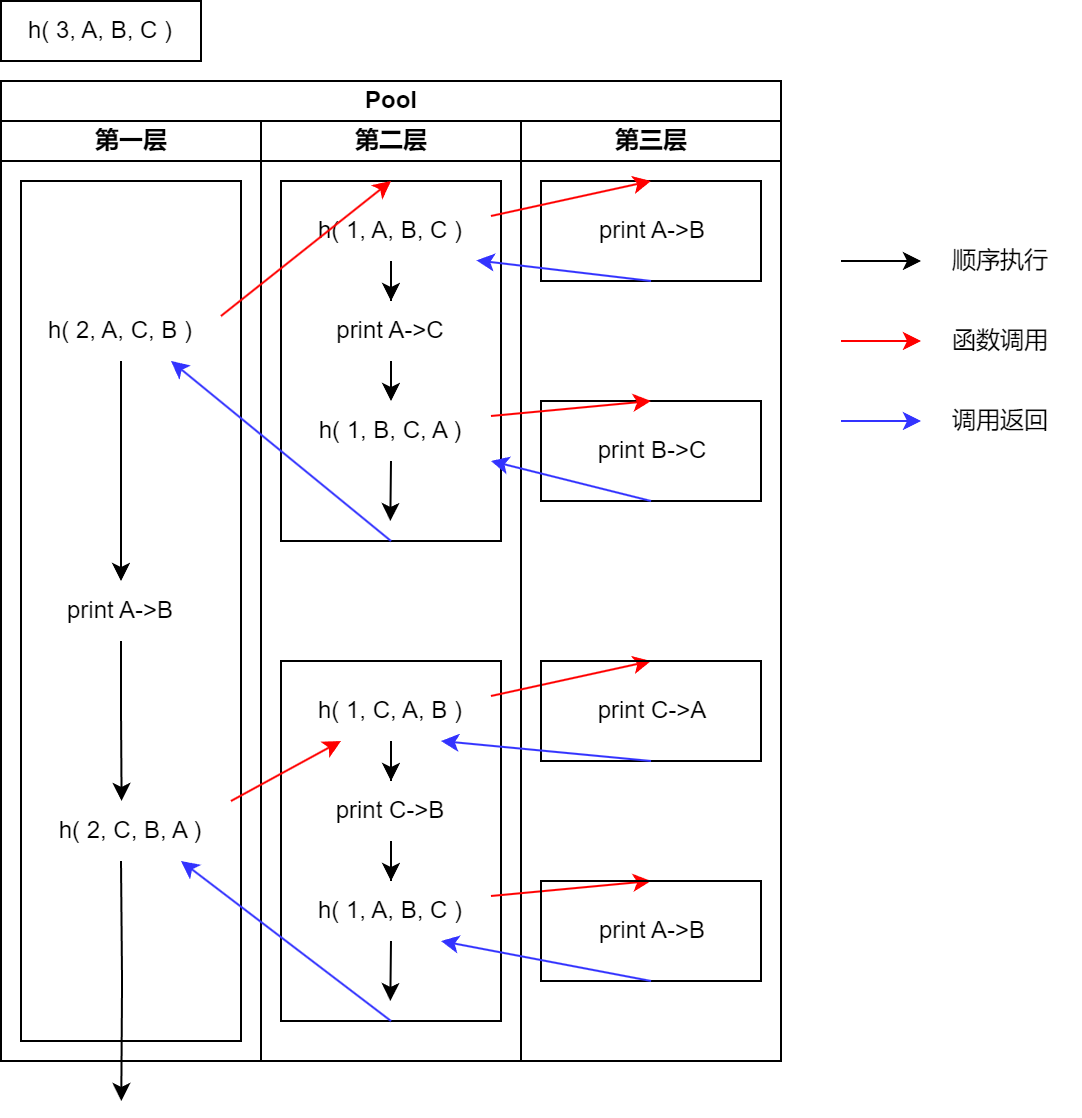
汉诺塔的调用过程
汉诺塔的调用过程

函数h的代码是一样的，只不过参数有所不同，图里已经把具体的参数填入对应的语句中了，实际代码中是由参数控制的，这点请注意。

我们先看代码，几个参数用n，from，to，idel分别表示盘子的数目，源杆，目标杆，空闲杆。 我们用伪代码来表示：

void h( int n, char from, char to, char idel){
    if( n==1 ){
        printf("%c->%c\n", from, to ); // 直接移动
        return;
    }
    h( n-1, from, idel, to ); // 利用 to 将 n-1个盘子从from 移动到 idel
    printf("%c->%c\n", from, to ); // 移动最下方的一个盘子
    h( n-1, idel, to, from ); // 利用 from 将 n-1个盘子从idel 移到 to
}

例如对于第一层h(3, A, B, C)的这层调用，会执行三条语句：

h(2, A, C, B);
print A->B
h(2, C, B, A);

这其中当执行第一条语句时，会进入一个新的h的调用。 在整个调用没有返回之前，程序不会执行下面的第二条print语句！ 请注意这点。

换句话说，整个图的上半部分，实际上都处于h(2,A,C,B)的范围。在这个函数的调用中只可能出现两种情况：

  1. n!=1，此时会继续触发h的调用，换句话说程序运行通过这个调用不断地展开，那么这个展开到什么时候能停止呢？
  2. n==1，直接移动，然后停机。通过停机条件停止展开过程并返回。

所以现在能够明白为什么说递归只要写好递推和停机条件就可以自动运行了吧！ 这两个部分缺一不可，缺少递推，整个过程就不能自动展开。缺少停机条件，这个过程就停不下来！

自己试一下！

再次强调，我可以把教程写得尽可能清楚，然而正如开篇所说：迭代是属于凡人的，而递归属于神的。

递归是一种与你之前掌握的编码方式完全相反的思维方式。你不可能不跑代码就掌握它！

自己在调试器里跑一下胜过仔细读这段内容10倍。还可以进一步锻炼你的调试能力。

在这个过程中，打开调用栈的调试窗口会有助于你了解执行过程。

计算机如何执行递归

如果到这里你都可以跟上。那么我就可以解释一下递归到底如何执行的了。

仔细研究过整个过程之后，你应该会有一种感觉：递归在执行下一层调用时，好像把本层函数卡在调用的部分了，等调用返回时再继续执行。

换句话说当函数调用时，当前的状态被缓存起来了，等返回后恢复状态再继续执行。

你的感觉没错！对数据结构有一定了解的童鞋一定知道这种记住当前状态，或者说回溯需要什么来实现——就是栈。

其实每个调试器都有一个工具叫调用栈。这个实际上并不是调试器的功能，而是函数调用就是这么做的。

我们可以画出上面那个调用过程中，调用栈的变化过程，帮助你理解整个步骤如何执行的：

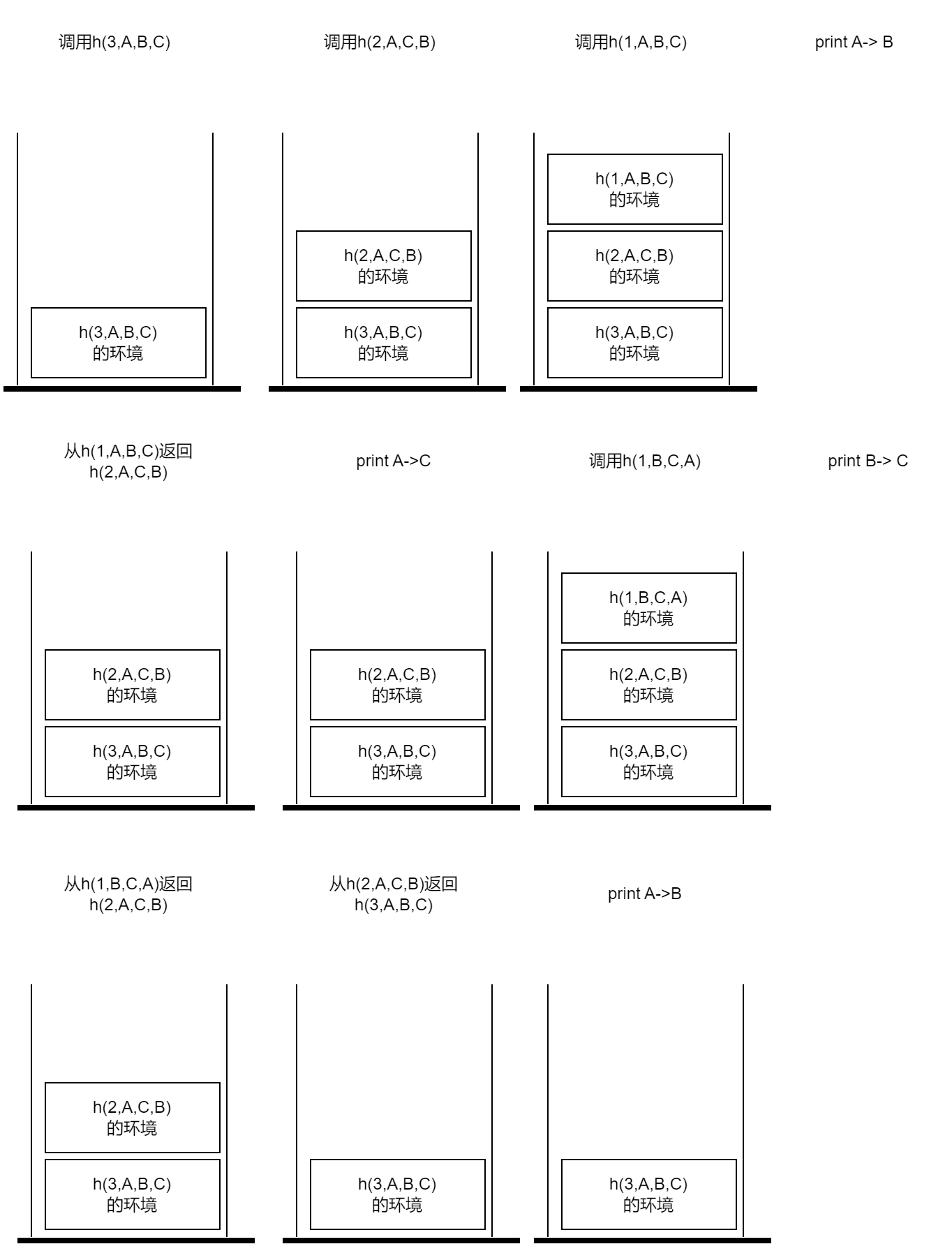
调用栈的变化过程
调用栈的变化过程

限于篇幅仅画出上半部分的调用过程，请你自己画出下半部分以加深自己的理解。

递归的代价

到这里我们就可以明白递归的代价是什么了：就是调用栈保存并恢复环境的开销，也就是函数调用的开销。

与迭代相比，递归会产生非常频繁的函数调用——而不要以为函数调用是免费的。

栈帧的大小也不是无限的，所谓函数的调用环境，既包括PC指针的位置，也包括局部变量的空间开销，这个开销有时候比你想象的大。

所以如果递归调用的层次过深，栈帧可能会被消耗殆尽（尤其处于调试模式下），从而导致程序非法退出。

不过这一切一般都是在生产环境才需要考虑，你们目前应该做的是：尽可能地掌握递归。

加深一下理解

试着自己分析一下递归反转字符串的代码。用一个简单的例子，例如4~6个字符的字符串，画一下调用的过程和对应的调用栈。

什么是递归

到这里我们可以再问一句，什么是递归？

或者我用一个比喻来结束本章：假如解决某个问题的步骤是一棵树，树的根是问题的解，树的叶子是解决问题所需要的材料。

那么：迭代和递归，哪个的思维方式是从根到叶子，哪个的思维方式是从叶子到根呢？

点击看答案
递归是从根到叶子，迭代时从叶子到根。

递归从全体向局部，迭代从局部向整体。

或者用计算机的术语：递归自顶向下，迭代自底向上——注意计算机的树是向下长的。

网页设计-电子讲义
Copyright © 2024 xmut-lby